Primero empezaremos por definir algunos términos y conceptos que se deben conocer sobre los caminos.
Un camino
En un grafo G es una sucesión finita de vértices y aristas alternos, donde cada arista tiene por extremos los vértices adyacentes.
(v0, v0v1, v1, v1v2,..., vn-1, vn-1vn, vn)
A v0 y vn se les denomina extremos del camino.
Longitud del camino
Es el número de aristas que contiene.
Camino cerrado
Los extremos coinciden, v0=vn, son el principio y el final del grafo
En un grafo, un camino puede expresarse por la sucesión de vértices
(v0, v1,..., vn-1, vn)
Camino simple:
En la sucesión de vértices no hay ninguno repetido.
Grafo dirigido
Un grafo dirigido es aquel en el que un nodo tiene un lazo y un grafo no dirigido es el que no tiene lazos y o sea que no apunta a si mismo.
Camino Euleriano
Inicio del problema
El origen de la teoría de los caminos eulerianos fue planteado y resuelto por el propio Leonhard Euler en 1736 en un problema que tiene el nombre de Siete puentes de la ciudad de Königsberg (Prusia oriental en el siglo XVIII y actualmente, Kaliningrado, provincia rusa) dando origen a la Teoría de los grafos.
El problema se enuncia de la siguiente forma: Dos islas en el río Pregel, en Königsberg se unen entre ellas y con la tierra firme mediante siete puentes. ¿Es posible dar un paseo empezando por una cualquiera de las cuatro partes de tierra firme, cruzando cada puente una sola vez y volviendo al punto de partida?

Euler enfocó el problema representando cada parte de tierra por un punto y cada puente, por una línea, uniendo los puntos que se corresponden. Entonces, el problema anterior se puede trasladar a la siguiente pregunta: ¿se puede recorrer el dibujo sin repetir las líneas?
Euler demostró que no era posible puesto que el número de líneas que inciden en cada punto no es par (condición necesaria para entrar y salir de cada punto, y para regresar al punto de partida, por caminos distintos en todo momento).
Camino euleriano
En la teoría de los grafos , un camino euleriano es un camino en un grafo que visita cada arista una sola vez.
Para que un en un grafo haya un camino euleriano deben de cumplirse las siguientes condiciones:
- Un grafo no dirigido contiene un ciclo euleriano si y sólo si (1) es conexo y (2) cada vértice es de grado par.
- Un grafo no dirigido contiene un camino euleriano si y sólo si (1) es conexo y (2) todos menos dos vértices son de grado par. Estos dos vértices serán los puntos de inicio y final de la ruta.
- Por último, un grafo dirigido contiene un camino euleriano si y sólo si (1) es conexo y (2) todos menos dos vértices tienen el mismo grado y estos dos tienen sus vértices en grados diferentes
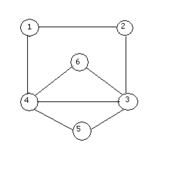
En la imagen P = {1,2,3,4,6,3,5,4,1} es un camino euleriano.El camino empieza en el nodo 1 va hacia el nodo 2, después va hacia el nodo 3, después sigue hacia el nodo 4, después va hacia el nodo 6 y regresa al nodo 3 después va hacia el nodo 5 después al 4 y finalmente llega al nodo de inicio el 1.
El siguiente video explica como funciona el algoritmo:
Complejidad del algoritmo
El número de circuitos de Euler en dígrafos se puede calcular utilizando el llamado teorema de BEST , nombrado después de ruijn B , van-E hrenfest Aardenne , mito S y T utte . La fórmula establece que el número de circuitos euleriano en un digrafo es el producto de los factoriales cierto grado y el número de raíces arborescencias . Este ultimo puede ser computado como factor determinante,por el teorema de arbol de la matriz, dando un algoritmo de tiempo polinomico.
Bibliografía

.bmp)
.bmp)